470. Суперпалиндромы
Назовём палиндромом
строку длиной более одного символа, которая одинаково читается как справа
налево, так и слева направо. Суперпалиндромом будем называть строку, которую можно
представить как конкатенацию одного или нескольких палиндромов.
Дана строка s. Найдите
количество подстрок в s, которые являются суперпалиндромами.
Вход. Строка s состоит из последовательности от 1 до 1000
строчных латинских букв без пробелов.
Выход. Выведите одно
число – количество подстрок строки s, являющихся суперпалиндромами.
|
Пример
входа |
Пример
выхода |
|
abacdc |
3 |
РЕШЕНИЕ
динамическое
программирование - палиндромы
Анализ алгоритма
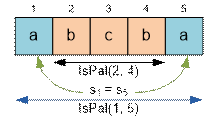
Пусть s – входная строка. Подстрока si … sj является палиндромом, если выполняется одно из следующих условий:
·
i ≥ j (подстрока пустая или состоит из одного
символа);
·
si = sj и подстрока si+1…sj-1 является
палиндромом;
Пусть функция
IsPal(i, j) возвращает 1, если si…sj является палиндромом, и 0
иначе. Значения IsPal(i, j)
запоминаем в ячейках pal[i][j].
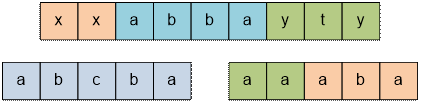
Строка является
суперпалиндромом, если её можно представить в виде конкатенации одного или более палиндромов. Например,
следующие строки являются суперпалиндромами:
Пусть dp[i][j]
= 1, если подстрока si…sj (i < j) является
суперпалиндромом и dp[i][j] = 0 иначе. Переберем все пары (i, j) для 0 ≤ i < j < n, и если
подстрока si…sj является палиндромом, то она также является и
суперпалиндромом, поэтому установим dp[i][j] = 1. Отметим, что dp[i][j]
= 0 при i ≥ j. Слово из одной буквы палиндромом не
считается, поэтому как частный случай имеем dp[i][i] = 0.
Для каждой пары
(i, j) переберем все возможные значения k (i < k < j – 1) и если si…sk и sk+1…sj
являются суперпалиндромами (и состоят из более чем одного символа вследствие
ограничения на k), то и si…sj является суперпалиндромом.
Остается
подсчитать количество пар (i, j), для которых i < j и dp[i][j]
= 1. Это число и есть ответ.
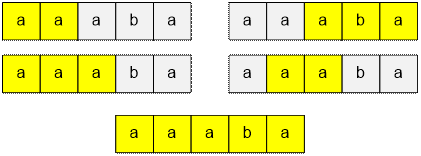
Пример
Для заданного примера – строки “abacdc”, имеются 3 подстроки, являющиеся суперпалиндромами:
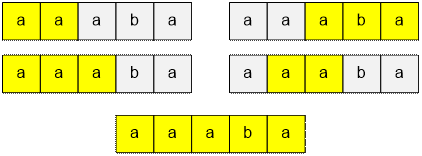
Для строки “aaaba” имеется 5 подстрок, которые являются суперпалиндромами:
Реализация алгоритма
Объявим рабочие
массивы.
#define MAX 1010
char s[MAX];
int dp[MAX][MAX];
int pal[MAX][MAX];
Функция IsPal(i, j)
проверяет, является ли подстрока si…sj палиндромом. Подстрока si … sj является палиндромом, если si = sj
и si+1…sj-1 является
палиндромом. Значения IsPal(i, j) запоминаем в ячейках массива pal[i][j].
int IsPal(int
i, int j)
{
if (i >=
j) return pal[i][j] = 1;
if (pal[i][j]
!= -1) return pal[i][j];
return
pal[i][j] = (s[i] == s[j]) && IsPal(i+1,j-1);
}
Основная часть
программы. Читаем входную строку.
gets(s); n =
strlen(s);
memset(dp,0,sizeof(dp));
memset(pal,-1,sizeof(pal));
Переберем все пары (i,
i + len) по возрастанию длин интервалов.
for (len = 1; len < n; len++)
for (i = 0; i + len < n; i++)
{
j = i + len;
Подстрока si…sj содержит более одного
символа. Если она палиндром, то она и суперпалиндром.
if
(IsPal(i,j))
{
dp[i][j] = 1;
continue;
}
Если si…sk и sk+1…sj суперпалиндромы, то si…sj является суперпалиндромом.
for(k = i +
1; k < j - 1; k++)
if(dp[i][k]
&& dp[k + 1][j])
{
dp[i][j] = 1;
break;
}
}
Подсчитываем количество суперпалиндромов.
res = 0;
for (i = 0; i < n; i++)
for (j = i+1; j < n;
j++)
res += dp[i][j];
Выводим ответ.
printf("%d\n",res);
Реализация алгоритма – рекурсивная
Объявим входную
строку s и
рабочие массивы.
#define MAX 1010
string s;
int dp[MAX][MAX], pal[MAX][MAX];
Функция IsPal(i, j)
проверяет, является ли подстрока si…sj палиндромом. Подстрока si … sj является палиндромом, если si = sj
и si+1…sj-1 является
палиндромом. Значения IsPal(i, j) запоминаем в ячейках массива pal[i][j].
int IsPal(int
i, int j)
{
if (i >=
j) return pal[i][j] = 1;
if (pal[i][j]
!= -1) return pal[i][j];
return
pal[i][j] = (s[i] == s[j]) && IsPal(i+1,j-1);
}
Функция f(i, j) возвращает 1, если si…sj является суперпалиндромом.
int f(int
i, int j)
{
Суперпалиндром должен содержать более одного символа.
if (i == j) return dp[i][j] = 0;
Если значение f(i, j) уже вычислено ранее, то возвращаем
его значение.
if (dp[i][j]
!= -1) return dp[i][j];
Если подстрока si…sj (i < j) является
палиндромом, то она является и суперпалиндромом.
if
(IsPal(i,j)) return dp[i][j] = 1;
Если si…sk (i < k) палиндром, а sk+1…sj (k + 1 < j) суперпалиндром, то si…sj является
суперпалиндромом.
for (int k = i + 1; k < j - 1; k++)
if (IsPal(i,k)
&& f(k + 1,j)) return dp[i][j] = 1;
Если ни одно из выше
описанных условий не выполняется, то si…sj не является суперпалиндромом.
return
dp[i][j] = 0;
}
Основная часть программы. Читаем входную строку s и вычисляем ее длину n.
cin >> s; n = s.size();
Инициализируем массивы dp и pal.
memset(dp,-1,sizeof(dp));
memset(pal,-1,sizeof(pal));
В переменой res подсчитываем
количество суперпалиндромов.
res = 0;
for (i = 0; i <
n; i++)
for (j = i + 1; j
< n; j++)
res += f(i,j);
Выводим ответ.
cout << res << endl;
Java реализация
import java.util.*;
public class Main
{
static
String s;
static int dp[][],
pal[][];
static int
IsPal(int i, int j)
{
if (i
>= j) return pal[i][j] =
1;
if (pal[i][j] !=
-1) return pal[i][j];
if (s.charAt(i) == s.charAt(j)
&& IsPal(i+1,j-1)
== 1) pal[i][j] =
1;
else pal[i][j] =
0;
return pal[i][j];
}
static int f(int i, int j)
{
if (i == j) return dp[i][j] =
0;
if (dp[i][j] !=
-1) return dp[i][j];
if (IsPal(i,j) ==
1) return dp[i][j] =
1;
for(int k = i + 1;
k < j - 1; k++)
if(IsPal(i,k) == 1
&& f(k + 1,j) ==
1) return dp[i][j] =
1;
return dp[i][j] =
0;
}
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
s = con.nextLine();
int n = s.length();
dp = new int[n][n];
pal = new int[n][n];
for(int i = 0;
i < n; i++)
for(int j = 0;
j < n; j++)
{
dp[i][j] =
-1;
pal[i][j] =
-1;
}
int res = 0;
for(int i = 0;
i < n; i++)
for(int j = i+1; j <
n; j++)
res += f(i,j);
System.out.println(res);
con.close();
}
}